Jan
17
p.s. @ 20100119 这是前几天写的,本来打算给godaddy加一个sockets扩展,但是失败了,还是发出来,记录一下。
godaddy的虚拟主机给的权限真是宽,允许自定义php.ini。
自定义的php.ini默认放在$HOME/html/php.ini,这个是针对php4的,我选择的是php5,所以应该是php5.ini。
//以下在虚拟主机上操作
$ cd ~/html
$ cp /web/conf/php5.ini .
$ vi php5.ini
然后修改max post size之类的参数吧~过一小段时间,再看phpinfo(),就出效果了。
编译php扩展的步骤
$ wget http://museum.php.net/php5/php-5.2.8.tar.bz2 //godaddy上面的是5.2.8, i386
$ tar jxf php-5.2.8.tar.bz2
$ cd php-5.2.8/ext/sockets
$ phpize //注意,需要安装php5-dev (apt-get install php5-dev)
$ ./configure --with-php-config=/usr/bin/php-config (最好$ whereis php-config 看一下路径)
$ make
拷贝到godday去
$ scp modules/sockets.so yourname@yourdomain:~/
然后修改php5.ini,增加
extension=sockets.so
发现无法正常加载,失望=。=
godaddy的虚拟主机给的权限真是宽,允许自定义php.ini。
自定义的php.ini默认放在$HOME/html/php.ini,这个是针对php4的,我选择的是php5,所以应该是php5.ini。
//以下在虚拟主机上操作
$ cd ~/html
$ cp /web/conf/php5.ini .
$ vi php5.ini
然后修改max post size之类的参数吧~过一小段时间,再看phpinfo(),就出效果了。
编译php扩展的步骤
$ wget http://museum.php.net/php5/php-5.2.8.tar.bz2 //godaddy上面的是5.2.8, i386
$ tar jxf php-5.2.8.tar.bz2
$ cd php-5.2.8/ext/sockets
$ phpize //注意,需要安装php5-dev (apt-get install php5-dev)
$ ./configure --with-php-config=/usr/bin/php-config (最好$ whereis php-config 看一下路径)
$ make
拷贝到godday去
$ scp modules/sockets.so yourname@yourdomain:~/
然后修改php5.ini,增加
extension=sockets.so
发现无法正常加载,失望=。=
Jan
15
从标题就可以看出来,这篇的内容是大杂烩,主要是这几天玩的东西,一并说一下
总共5个东西
1. 交换分区
第三篇说的重新分区太危险了,万一SmartQ升级固件的程序不认,那就挂了。所以决定把那128MB拿来做交换分区。具体做法如下
建立一个100MB的文件
# dd if=/dev/zero of=/media/ndda2/swapfile bs=1MB count=100
格式化成swap所需的格式
# mkswap /media/ndda2/swapfile
# swapon /media/ndda2/swapfile
如果不需要了,可以这样
# swapoff /media/ndda2/swapfile
可以把这个写入rc.local.
2. 键位映射
其实主要是xmodmap和xev这2个东西
先讲xev吧:
$ xev | grep keycode
然后按现有的几个键,可以看到,屏幕左边的三个分别是(112)Prior, (117)Next, (64)Alt,上面的三个(从左到右)分别是(124)XF86PowerOff(关机), (9)Esc, (36)Return(回车)。所以实际上可以用ALT+ESC来切换程序。
$ xmodmap -pke
可以看到现在的keycode被映射成什么东西
$ xmodmap -e 'keycode 112 = Up'
$ xmodmap -e 'keycode 117 = Down'
这样就可以把那两个按键变成上下,而不是翻页了。
$ xmodmap -e 'keycode 112 = Prior'
$ xmodmap -e 'keycode 117 = Next'
这样还原。
3. 快捷键
主要是修改 /home/user/.config/openbox/lxde-rc.xml
找到Keybinding这一节,按照格式修改即可。
比如默认的A-XF86PowerOff(Alt+Power组合键)是运行ts_calibrate,就是校正屏幕的,但是其实这个基本用不到,所以可以改成其他的,比如改成vlc,或者fbreader;默认的XF86PowerOff是打开那个系统设置(coman)程序,很容易被误按,我也改掉了。这样就多了2个可以自定义的快捷键,很爽。有兴趣的话还可以研究一下怎么增加其他组合按键,比如Alt+Enter :)
p.s. 需要运行一次首选项->窗口设置 才可以生效。
4. 虚拟键盘
系统自带的虚拟键盘是matchbox-keyboard, Nokia的N770什么的也在用。键盘的布局文件是存放在/usr/share/matchbox-keyboard这个目录下的,标准键盘用的就是keyboard.xml这个文件了。可以修改这个文件来实现自己想要的键位布局。昨天整了一个接近标准PC键盘的键位布局,效果见图: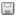 下载文件 (已下载 1881 次)
下载文件 (已下载 1881 次)

5. 一个脚本,我存放在/usr/bin/run_app,然后XF86PowerOff映射为运行这个脚本,效果就是,按一下启动vlc,再按一下结束vlc。
总共5个东西
1. 交换分区
第三篇说的重新分区太危险了,万一SmartQ升级固件的程序不认,那就挂了。所以决定把那128MB拿来做交换分区。具体做法如下
建立一个100MB的文件
# dd if=/dev/zero of=/media/ndda2/swapfile bs=1MB count=100
格式化成swap所需的格式
# mkswap /media/ndda2/swapfile
# swapon /media/ndda2/swapfile
如果不需要了,可以这样
# swapoff /media/ndda2/swapfile
可以把这个写入rc.local.
2. 键位映射
其实主要是xmodmap和xev这2个东西
先讲xev吧:
$ xev | grep keycode
然后按现有的几个键,可以看到,屏幕左边的三个分别是(112)Prior, (117)Next, (64)Alt,上面的三个(从左到右)分别是(124)XF86PowerOff(关机), (9)Esc, (36)Return(回车)。所以实际上可以用ALT+ESC来切换程序。
$ xmodmap -pke
可以看到现在的keycode被映射成什么东西
$ xmodmap -e 'keycode 112 = Up'
$ xmodmap -e 'keycode 117 = Down'
这样就可以把那两个按键变成上下,而不是翻页了。
$ xmodmap -e 'keycode 112 = Prior'
$ xmodmap -e 'keycode 117 = Next'
这样还原。
3. 快捷键
主要是修改 /home/user/.config/openbox/lxde-rc.xml
找到Keybinding这一节,按照格式修改即可。
比如默认的A-XF86PowerOff(Alt+Power组合键)是运行ts_calibrate,就是校正屏幕的,但是其实这个基本用不到,所以可以改成其他的,比如改成vlc,或者fbreader;默认的XF86PowerOff是打开那个系统设置(coman)程序,很容易被误按,我也改掉了。这样就多了2个可以自定义的快捷键,很爽。有兴趣的话还可以研究一下怎么增加其他组合按键,比如Alt+Enter :)
p.s. 需要运行一次首选项->窗口设置 才可以生效。
4. 虚拟键盘
系统自带的虚拟键盘是matchbox-keyboard, Nokia的N770什么的也在用。键盘的布局文件是存放在/usr/share/matchbox-keyboard这个目录下的,标准键盘用的就是keyboard.xml这个文件了。可以修改这个文件来实现自己想要的键位布局。昨天整了一个接近标准PC键盘的键位布局,效果见图:
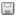 下载文件 (已下载 1881 次)
下载文件 (已下载 1881 次)5. 一个脚本,我存放在/usr/bin/run_app,然后XF86PowerOff映射为运行这个脚本,效果就是,按一下启动vlc,再按一下结束vlc。
#!/bin/bash
dir=$HOME/tmp
tmp=$dir/run_app.pid
if [ ! -d $dir ]; then
mkdir -p $dir
fi
if [ -f $tmp ]; then
kill `cat $tmp`
rm $tmp -rf
else
setsid vlc &
echo $! > $tmp
fi
dir=$HOME/tmp
tmp=$dir/run_app.pid
if [ ! -d $dir ]; then
mkdir -p $dir
fi
if [ -f $tmp ]; then
kill `cat $tmp`
rm $tmp -rf
else
setsid vlc &
echo $! > $tmp
fi
Jan
11
更多内容,参见laruence大牛的这篇: http://www.laruence.com/2009/07/23/994.html
这么短一段代码,有这么多考究的地方,很值得学习:
1. 5381
2. hash << 5 + hash --> hash * 33 (times 33算法)
3. -= 8
4. switch, break
...
这么短一段代码,有这么多考究的地方,很值得学习:
1. 5381
2. hash << 5 + hash --> hash * 33 (times 33算法)
3. -= 8
4. switch, break
...
static inline ulong zend_inline_hash_func(char *arKey, uint nKeyLength)
{
register ulong hash = 5381;
/* variant with the hash unrolled eight times */
for (; nKeyLength >= 8; nKeyLength -= 8) {
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
}
switch (nKeyLength) {
case 7: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 6: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 5: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 4: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 3: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 2: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 1: hash = ((hash << 5) + hash) + *arKey++; break;
case 0: break;
EMPTY_SWITCH_DEFAULT_CASE()
}
return hash;
}
{
register ulong hash = 5381;
/* variant with the hash unrolled eight times */
for (; nKeyLength >= 8; nKeyLength -= 8) {
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
hash = ((hash << 5) + hash) + *arKey++;
}
switch (nKeyLength) {
case 7: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 6: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 5: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 4: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 3: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 2: hash = ((hash << 5) + hash) + *arKey++; /* fallthrough... */
case 1: hash = ((hash << 5) + hash) + *arKey++; break;
case 0: break;
EMPTY_SWITCH_DEFAULT_CASE()
}
return hash;
}
Jan
10
第二篇把所有分区的大小都列出来了,不过还是漏了一点:
所有分区加起来,总共是1795,但是2G,用硬件厂商的单位换算,就是2,000,000,000B = 1907.35MB,而fdisk显示的是1883 MB,至少还应该有88MB的空间。
fdisk -l /dev/ndda没有看到另外的分区,根据block的数量来算,也没有找到这么大的地方,看起来应该是被隐藏了。不过还是可以大概估计出来这这88MB的用处——那就是用于WinCE的固件。当然,也可能是用于Android的固件,但是2个都用上空间不够大。而且WinCE的那个分区只用了2M多,说明固件肯定另外存了一份;而ndda4下面的4个逻辑分区都是Linux分区,所以肯定不会存在这里。综合一下,我觉得这88MB就是用来刷WinCE的固件了,而Andoid的,都放在ndda4里头。
由于我对Andoid没什么兴趣,决定把那467的空间搞出来。
注意:以下操作具有危险性,不熟悉Linux的同学,最好小心点儿,出了问题我可不负责,嗯。
具体的操作为:
1. 删除ndda4原有的分区
2. 建立一个新的分区
3. 格式化
4. 其他
第一步,用fdisk。说实话这是我第一次用linux下的fdisk=。= 不过还是挺简单的,如果有一些主分区、扩展分区、逻辑分区的知识的话。
V7里头这个Ubuntu它貌似是不支持卡上的逻辑分区的,ls /dev没能看到ndda5~ndda8就说明了问题。
所以应该把45678都给删掉,然后重新建立ndda4
具体操作:
root@SmartQ:/media# fdisk /dev/ndda
The number of cylinders for this disk is set to 57472.
There is nothing wrong with that, but this is larger than 1024,
and could in certain setups cause problems with:
1) software that runs at boot time (e.g., old versions of LILO)
2) booting and partitioning software from other OSs
(e.g., DOS FDISK, OS/2 FDISK)
Command (m for help):
这里可以输入m看看有哪些命令,输入d是删除分区:
Command (m for help): d
Partition number (1-8): 8
Command (m for help): d
Partition number (1-7): 7
Command (m for help): d
Partition number (1-6): 6
Command (m for help): d
Partition number (1-5): 5
Command (m for help): d
Partition number (1-4): 4
至此不需要的分区全都删掉了。然后看看现在的分区,命令是p,显示大致是这样的:
Disk /dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16
Partition 3 does not end on cylinder boundary.
注意这个42528,是分区3的末尾,我们接下来需要创建一个分区4,从42529开始,命令是n
Command (m for help): n
Command action
e extended
p primary partition (1-4)
p #需要创建一个主分区,输入,这里输入p
Selected partition 4
First cylinder (2-57472, default 2): 42529 #这里输入开始
Last cylinder, +cylinders or +size{K,M,G} (42529-57472, default 57472): #直接回车,默认是到末尾
Using default value 57472
Command (m for help): p #再看一下,已经创建好了。
Disk /dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16
Partition 3 does not end on cylinder boundary.
/dev/ndda4 42529 57472 478208 83 Linux
Partition 4 does not end on cylinder boundary.
#接下来这里一定要慎重!!如果不确定,可以输入q退出,前面所有的都不算数
Command (m for help): w #存盘
完了以后
#sync
#init 6 #重启命令
等到重启好了,格式化,挂载:
# mkfs.ext3 /dev/ndda4
# mkdir /media/ndda4
# mount -t ext3 /dev/ndda4 /media/ndda4
如果不想每次启动都这么弄,可以加入fstab
# vi /etc/fstab
增加一行
/dev/ndda4 /media/ndda4 ext3 defaults 0 0
:wq存盘退出,然后
# mount -a
在/media/ndda4下面就可以访问这个分区了。
到这里,手头的V7就多了一个可用的467MB的分区,爽!经过测试,Android已经不能启动了,而CE仍然没有问题 :)
-------------华丽的分割线--------------
接下来再做一些小改造:
1. 把ndda4挂载到/home分区,而不是只有128MB的ndda2
2. 把ndda2格式化成fat32,给WinCE用(后来发现一个问题,不建议这么整,详情见后文)
具体操作:
# mkdir /media/ndda2
# vi /home/fstab
原先home那一行和ndda4的那一行注释掉(就是前面加一个#就可以了),然后加上这两行:
/dev/ndda4 /home ext3 noatime 0 2
/dev/ndda2 /media/ndda2 vfat defaults 0 0
:wq存盘退出
然后
# cp -r /home/user /media/ndda4
# sync
# init 6 (重启命令)
重启以后,挂载在/home的就是/dev/ndda4了,空间大多了吧 哇哈哈
然后
# apt-get install dosfstools
安装好以后就有mkfs.vfat和mkfs.msdos了。
# mkfs.vfat /dev/ndda2
格式化成fat32文件系统
# mount -a
这样就挂上去了。
重启到WinCE下面,你会发现,怎么什么设置都没有了,先校准一下屏幕,打开“我的设备”,会发现一个新的NAND分区,里面是原先CE下的设置和文件。也就是说,WinCE在引导的时候,会在找到的第一个可用分区建立自己的目录结构,把那里当作自己的家。。。所以如果你不想把WinCE重新设置一边的话,建议还是不要这么搞了。此外,这样做可能还有一个问题:如果重新刷Ubuntu,可能会导致ndda2被重新格式化成linux分区,然后WinCE就会在NAND(也就是ndda3)上面再搞他自己的帝国了。
同时这也给我们一个启示:要将WinCE恢复原状,根本不需要重新刷机,只要在Ubuntu下挂载ndda3分区,把它全部清空,然后重启进入WinCE,就是全新的了。
OVER。
第四篇预告:重新划分所有分区。这个还真的有点危险了,我要仔细考虑一下是否有需要这么做。其实我是想把UBuntu的根分区扩容。
所有分区加起来,总共是1795,但是2G,用硬件厂商的单位换算,就是2,000,000,000B = 1907.35MB,而fdisk显示的是1883 MB,至少还应该有88MB的空间。
fdisk -l /dev/ndda没有看到另外的分区,根据block的数量来算,也没有找到这么大的地方,看起来应该是被隐藏了。不过还是可以大概估计出来这这88MB的用处——那就是用于WinCE的固件。当然,也可能是用于Android的固件,但是2个都用上空间不够大。而且WinCE的那个分区只用了2M多,说明固件肯定另外存了一份;而ndda4下面的4个逻辑分区都是Linux分区,所以肯定不会存在这里。综合一下,我觉得这88MB就是用来刷WinCE的固件了,而Andoid的,都放在ndda4里头。
由于我对Andoid没什么兴趣,决定把那467的空间搞出来。
注意:以下操作具有危险性,不熟悉Linux的同学,最好小心点儿,出了问题我可不负责,嗯。
具体的操作为:
1. 删除ndda4原有的分区
2. 建立一个新的分区
3. 格式化
4. 其他
第一步,用fdisk。说实话这是我第一次用linux下的fdisk=。= 不过还是挺简单的,如果有一些主分区、扩展分区、逻辑分区的知识的话。
V7里头这个Ubuntu它貌似是不支持卡上的逻辑分区的,ls /dev没能看到ndda5~ndda8就说明了问题。
所以应该把45678都给删掉,然后重新建立ndda4
具体操作:
root@SmartQ:/media# fdisk /dev/ndda
The number of cylinders for this disk is set to 57472.
There is nothing wrong with that, but this is larger than 1024,
and could in certain setups cause problems with:
1) software that runs at boot time (e.g., old versions of LILO)
2) booting and partitioning software from other OSs
(e.g., DOS FDISK, OS/2 FDISK)
Command (m for help):
这里可以输入m看看有哪些命令,输入d是删除分区:
Command (m for help): d
Partition number (1-8): 8
Command (m for help): d
Partition number (1-7): 7
Command (m for help): d
Partition number (1-6): 6
Command (m for help): d
Partition number (1-5): 5
Command (m for help): d
Partition number (1-4): 4
至此不需要的分区全都删掉了。然后看看现在的分区,命令是p,显示大致是这样的:
Disk /dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16
Partition 3 does not end on cylinder boundary.
注意这个42528,是分区3的末尾,我们接下来需要创建一个分区4,从42529开始,命令是n
Command (m for help): n
Command action
e extended
p primary partition (1-4)
p #需要创建一个主分区,输入,这里输入p
Selected partition 4
First cylinder (2-57472, default 2): 42529 #这里输入开始
Last cylinder, +cylinders or +size{K,M,G} (42529-57472, default 57472): #直接回车,默认是到末尾
Using default value 57472
Command (m for help): p #再看一下,已经创建好了。
Disk /dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16
Partition 3 does not end on cylinder boundary.
/dev/ndda4 42529 57472 478208 83 Linux
Partition 4 does not end on cylinder boundary.
#接下来这里一定要慎重!!如果不确定,可以输入q退出,前面所有的都不算数
Command (m for help): w #存盘
完了以后
#sync
#init 6 #重启命令
等到重启好了,格式化,挂载:
# mkfs.ext3 /dev/ndda4
# mkdir /media/ndda4
# mount -t ext3 /dev/ndda4 /media/ndda4
如果不想每次启动都这么弄,可以加入fstab
# vi /etc/fstab
增加一行
/dev/ndda4 /media/ndda4 ext3 defaults 0 0
:wq存盘退出,然后
# mount -a
在/media/ndda4下面就可以访问这个分区了。
到这里,手头的V7就多了一个可用的467MB的分区,爽!经过测试,Android已经不能启动了,而CE仍然没有问题 :)
-------------华丽的分割线--------------
接下来再做一些小改造:
1. 把ndda4挂载到/home分区,而不是只有128MB的ndda2
2. 把ndda2格式化成fat32,给WinCE用(后来发现一个问题,不建议这么整,详情见后文)
具体操作:
# mkdir /media/ndda2
# vi /home/fstab
原先home那一行和ndda4的那一行注释掉(就是前面加一个#就可以了),然后加上这两行:
/dev/ndda4 /home ext3 noatime 0 2
/dev/ndda2 /media/ndda2 vfat defaults 0 0
:wq存盘退出
然后
# cp -r /home/user /media/ndda4
# sync
# init 6 (重启命令)
重启以后,挂载在/home的就是/dev/ndda4了,空间大多了吧 哇哈哈
然后
# apt-get install dosfstools
安装好以后就有mkfs.vfat和mkfs.msdos了。
# mkfs.vfat /dev/ndda2
格式化成fat32文件系统
# mount -a
这样就挂上去了。
重启到WinCE下面,你会发现,怎么什么设置都没有了,先校准一下屏幕,打开“我的设备”,会发现一个新的NAND分区,里面是原先CE下的设置和文件。也就是说,WinCE在引导的时候,会在找到的第一个可用分区建立自己的目录结构,把那里当作自己的家。。。所以如果你不想把WinCE重新设置一边的话,建议还是不要这么搞了。此外,这样做可能还有一个问题:如果重新刷Ubuntu,可能会导致ndda2被重新格式化成linux分区,然后WinCE就会在NAND(也就是ndda3)上面再搞他自己的帝国了。
同时这也给我们一个启示:要将WinCE恢复原状,根本不需要重新刷机,只要在Ubuntu下挂载ndda3分区,把它全部清空,然后重启进入WinCE,就是全新的了。
OVER。
第四篇预告:重新划分所有分区。这个还真的有点危险了,我要仔细考虑一下是否有需要这么做。其实我是想把UBuntu的根分区扩容。
Jan
10
(这篇文章已经在bbs.zhiqi.com.cn发出去了,在这里润色一下再贴出来)
前面已经把openssh-server搞定了,接下来看看里头的东西。智器官方的介绍说的是2G的空间,其中用户可用128MB,听起来太少了。那其他的空间都哪里去了呢,看看先。
#df -lh 可以看到
Filesystem Size Used Avail Use% Mounted on
/dev/ndda1 1.1G 579M 450M 57% / #这个是Ubuntu的根分区,用了579M,还有450M可用
/dev/ndda2 124M 13M 106M 11% /home #这个是用户分区,124(其实是128M,其中4M文件系统用了吧)
/dev/ndda3 99M 2.1M 97M 3% /media/tmp/ndda3 #这个是我自己挂载的,里面有Windows等内容,可以判断出来是WinCE的分区
/dev/mmcblk1p1 3.8G 2.7G 1.2G 71%
/media/MY FLASH DI #这个是SD卡 /dev/sda4 3.8G 2.5G 1.4G 66%
/media/WIN7 #这个是额外插上去的U盘,之所以识别成4,我想是因为前面已经有了123。
另外, # ls /dev 可以看到有个ndda,再 #fdisk -l /dev/ndda,可以看到
每个Block的大小是1024B,也就是1K,换算过来,从1~8共8个分区的大小是(MB)
1126400/1024=1100
131072/1024=128
102400/1024=100
478208/1024=467
125024/1024=122
156288/1024=152
58624/1024=57.25
138144/1024=134.91
其中第四个是扩展分区,其实就是后面四个逻辑分区的"合体",
很明显可以看出来各个分区的作用,已经标注在上面的引用里面了。
结论:
1. 第一个分区是Ubuntu的根分区,有450MB可用空间,多安一点软件其实没问题
2. 第二个分区是Ubuntu的/home分区,其实就是桌面上的我的文档,可用空间124MB,这就是官方宣称的128MB可用空间了
3. 第三个分区是Windows分区,有97MB的可用空间
4. 第四个分区的Andoid的,有467MB, 鉴于我觉得那个Andoid很鸡肋,完全可以拿来玩。
5. 综上所述,各个系统之间的可用空间是独立的。
下一步,准备拿/dev/ndda4开刀。
前面已经把openssh-server搞定了,接下来看看里头的东西。智器官方的介绍说的是2G的空间,其中用户可用128MB,听起来太少了。那其他的空间都哪里去了呢,看看先。
#df -lh 可以看到
引用
Filesystem Size Used Avail Use% Mounted on
/dev/ndda1 1.1G 579M 450M 57% / #这个是Ubuntu的根分区,用了579M,还有450M可用
/dev/ndda2 124M 13M 106M 11% /home #这个是用户分区,124(其实是128M,其中4M文件系统用了吧)
/dev/ndda3 99M 2.1M 97M 3% /media/tmp/ndda3 #这个是我自己挂载的,里面有Windows等内容,可以判断出来是WinCE的分区
/dev/mmcblk1p1 3.8G 2.7G 1.2G 71%
/media/MY FLASH DI #这个是SD卡 /dev/sda4 3.8G 2.5G 1.4G 66%
/media/WIN7 #这个是额外插上去的U盘,之所以识别成4,我想是因为前面已经有了123。
另外, # ls /dev 可以看到有个ndda,再 #fdisk -l /dev/ndda,可以看到
引用
root@SmartQ:/media/tmp# fdisk -l /dev/ndda Disk
/dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32 (Ubuntu /)
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16 (Ubuntu /home)
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16 (WinCE)
Partition 3 does not end on cylinder boundary.
/dev/ndda4 42529 57472 478208 5 Extended (扩展分区,肯定是Andoid的了)
Partition 4 does not end on cylinder boundary.
/dev/ndda5 42530 46436 125024 83 Linux
/dev/ndda6 46438 51321 156288 83 Linux
/dev/ndda7 51323 53154 58624 83 Linux
/dev/ndda8 53156 57472 138144 83 Linux
/dev/ndda: 1883 MB, 1883242496 bytes
1 heads, 64 sectors/track, 57472 cylinders
Units = cylinders of 64 * 512 = 32768 bytes
Disk identifier: 0x3079ae40
Device Boot Start End Blocks Id System
/dev/ndda1 33 35232 1126400 b W95 FAT32 (Ubuntu /)
Partition 1 does not end on cylinder boundary.
/dev/ndda2 35233 39328 131072 6 FAT16 (Ubuntu /home)
Partition 2 does not end on cylinder boundary.
/dev/ndda3 39329 42528 102400 6 FAT16 (WinCE)
Partition 3 does not end on cylinder boundary.
/dev/ndda4 42529 57472 478208 5 Extended (扩展分区,肯定是Andoid的了)
Partition 4 does not end on cylinder boundary.
/dev/ndda5 42530 46436 125024 83 Linux
/dev/ndda6 46438 51321 156288 83 Linux
/dev/ndda7 51323 53154 58624 83 Linux
/dev/ndda8 53156 57472 138144 83 Linux
每个Block的大小是1024B,也就是1K,换算过来,从1~8共8个分区的大小是(MB)
1126400/1024=1100
131072/1024=128
102400/1024=100
478208/1024=467
125024/1024=122
156288/1024=152
58624/1024=57.25
138144/1024=134.91
其中第四个是扩展分区,其实就是后面四个逻辑分区的"合体",
很明显可以看出来各个分区的作用,已经标注在上面的引用里面了。
结论:
1. 第一个分区是Ubuntu的根分区,有450MB可用空间,多安一点软件其实没问题
2. 第二个分区是Ubuntu的/home分区,其实就是桌面上的我的文档,可用空间124MB,这就是官方宣称的128MB可用空间了
3. 第三个分区是Windows分区,有97MB的可用空间
4. 第四个分区的Andoid的,有467MB, 鉴于我觉得那个Andoid很鸡肋,完全可以拿来玩。
5. 综上所述,各个系统之间的可用空间是独立的。
下一步,准备拿/dev/ndda4开刀。
Jan
10
因为在那个触摸屏上打字太痛苦了,于是决定安装一个openssh-server。
查看了一下/etc/apt/sources.list,内容只有一行原来是karmic,9.10了哇,真是与时俱进。直接用的官方源。
# sudo passwd root 随便给root设置一个简单的password
# su - 切换用户为root
#apt-get update 发现住处那个ooxx的长城宽带,连上去的速度大约是100B/s以内。很爽。
# apt-get update 带到公司再来,这已经是今天了=。=
# apt-get install openssh-server
openssh-server 已经是最新的版本了。
共升级了 0 个软件包,新安装了 0 个软件包, 要卸载 0 个软件包,有 80 个软件未被升级。
&*@$ 居然已经安装了,抑郁。
# /etc/init.d/ssh start
* Starting OpenBSD Secure Shell server sshd [ OK ]
然后在台式机上打开SecureCRT连上去,用户名密码就用root的那个,然后看到这个提示符,表示登录成功啦
root@SmartQ:~#
于是就不用忍受终端下用触摸屏打字的痛苦了..
p.s. 顺便安装了一些东西:gcc g++ build-essential vim ctags cscope,然后写了个hello smartq,没问题,嗯。以后应该会有用的,哇哈哈。另外,发现机器上已经有perl和python了,真是好东西哇好东西。
再p.s. apt安装的时候会先下载安装包,会放在/etc/cache/apt/archieves,如果确定不会删了再装,可以把它们都删掉 #apt-get clean,或者可以备份到卡上,免得下次下载很痛苦。
update 1 @ 2010-01-17
1. 更新源用国内的这个,速度很快
deb http://ubuntu.srt.cn/ubuntu-ports/ karmic main restricted universe multiverse
2. 安装个lrzsz,然后用SecureCRT连上去以后就很方便了
# sudo apt-get install lrzsz
# sz 文件名
可以下载到电脑上
# rz -e 回车
在电脑上选择文件,传输上去
查看了一下/etc/apt/sources.list,内容只有一行
引用
deb http://ports.ubuntu.com/ karmic main universe restricted multiverse
# sudo passwd root 随便给root设置一个简单的password
# su - 切换用户为root
#apt-get update 发现住处那个ooxx的长城宽带,连上去的速度大约是100B/s以内。很爽。
# apt-get update 带到公司再来,这已经是今天了=。=
# apt-get install openssh-server
openssh-server 已经是最新的版本了。
共升级了 0 个软件包,新安装了 0 个软件包, 要卸载 0 个软件包,有 80 个软件未被升级。
&*@$ 居然已经安装了,抑郁。
# /etc/init.d/ssh start
* Starting OpenBSD Secure Shell server sshd [ OK ]
然后在台式机上打开SecureCRT连上去,用户名密码就用root的那个,然后看到这个提示符,表示登录成功啦
root@SmartQ:~#
于是就不用忍受终端下用触摸屏打字的痛苦了..
p.s. 顺便安装了一些东西:gcc g++ build-essential vim ctags cscope,然后写了个hello smartq,没问题,嗯。以后应该会有用的,哇哈哈。另外,发现机器上已经有perl和python了,真是好东西哇好东西。
再p.s. apt安装的时候会先下载安装包,会放在/etc/cache/apt/archieves,如果确定不会删了再装,可以把它们都删掉 #apt-get clean,或者可以备份到卡上,免得下次下载很痛苦。
update 1 @ 2010-01-17
1. 更新源用国内的这个,速度很快
deb http://ubuntu.srt.cn/ubuntu-ports/ karmic main restricted universe multiverse
2. 安装个lrzsz,然后用SecureCRT连上去以后就很方便了
# sudo apt-get install lrzsz
# sz 文件名
可以下载到电脑上
# rz -e 回车
在电脑上选择文件,传输上去
Jan
10
昨天到中关村去,鼎好A2574试用了3个小时的SmartQ V7,然后终于决定买下来,一个V7,一个布袋,送一个烂耳机,一共1530。其间还有些纠结,反正没有买到可用的USB网卡,也没有买到想买的USB充电线,小抑郁。回来后在当当上买了一个KingMax的SDHC, 16GB, class6, 230。也就是总共花了接近1800。
折腾了很久,Ubuntu很慢,除去这个问题的话 用起来还算比较happy,此外就是屏幕不够大,那个键盘就占了好大的空间,很囧。之后试着看能不能把它转过来。WinCE软件不少,折腾起来阻力,而且全是玩软件,太无聊了。Android一点都不好玩。
后面慢慢贴一些“研究成果”出来
折腾了很久,Ubuntu很慢,除去这个问题的话 用起来还算比较happy,此外就是屏幕不够大,那个键盘就占了好大的空间,很囧。之后试着看能不能把它转过来。WinCE软件不少,折腾起来阻力,而且全是玩软件,太无聊了。Android一点都不好玩。
后面慢慢贴一些“研究成果”出来

Jan
7
编译apache的时候默认应该是有mod_cgi的,如果不确定,可以加上--enable_cgi。
在httpd.conf里面增加(或修改,因为可能已经有这个东西了):如果你修改了“某路径”,那么后面对应的Directory一节也应该对应修改
下面是一个简单的C编写的cgi程序,gcc -o printall simple_cgi.c,把printall放在cgi-bin目录下面。然后访问:http://localhost/cgi-bin/printall,可以看到输出。特别注意一下,cgi不仅要打HTTP实体,还要打HTTP头信息。如果你实在懒得写,在实体前面加上一个回车就行了:) 否则你会看到apache的error_log里输出诸如"malformed header from script. Bad header="这样的错误信息。
特别点出一下,GET请求的query_string是在environ["QUERY_STRING"]里面,而POST请求的输入,是从stdin中读取。
在httpd.conf里面增加(或修改,因为可能已经有这个东西了):
引用
ScriptAlias /cgi-bin/ /某路径/cgi-bin/
引用
<Directory "/某路径/cgi-bin">
AllowOverride None
Options FollowSymLinks #如果不放心,这里还可以加上一个ExecCgi选项。
Order allow,deny
Allow from all
</Directory>
AllowOverride None
Options FollowSymLinks #如果不放心,这里还可以加上一个ExecCgi选项。
Order allow,deny
Allow from all
</Directory>
下面是一个简单的C编写的cgi程序,gcc -o printall simple_cgi.c,把printall放在cgi-bin目录下面。然后访问:http://localhost/cgi-bin/printall,可以看到输出。特别注意一下,cgi不仅要打HTTP实体,还要打HTTP头信息。如果你实在懒得写,在实体前面加上一个回车就行了:) 否则你会看到apache的error_log里输出诸如"malformed header from script. Bad header="这样的错误信息。
#include <stdio.h>
#include <stdlib.h>
extern char ** environ;
int main ()
{
int i;
puts("Content-Type: text/plain\n\n");
for (i = 0; environ[i] != NULL; i++) {
printf ("%s\n", environ[i]);
}
if (strncmp("POST", getenv("REQUEST_METHOD"), 4) == 0) {
char buf[1025];
while (1) {
fgets(buf, 1024, stdin);
printf( "%s", buf);
if (feof(stdin)) {
break;
}
}
}
return 0;
}
#include <stdlib.h>
extern char ** environ;
int main ()
{
int i;
puts("Content-Type: text/plain\n\n");
for (i = 0; environ[i] != NULL; i++) {
printf ("%s\n", environ[i]);
}
if (strncmp("POST", getenv("REQUEST_METHOD"), 4) == 0) {
char buf[1025];
while (1) {
fgets(buf, 1024, stdin);
printf( "%s", buf);
if (feof(stdin)) {
break;
}
}
}
return 0;
}
特别点出一下,GET请求的query_string是在environ["QUERY_STRING"]里面,而POST请求的输入,是从stdin中读取。